哈希表
TIP
哈希表是一种无序的,key 值不允许重复的一种数据结构,表现为键值对(key-value),一般基于数组实现
优点
- 哈希表可以提供非常快速的插入-删除-查找操作
- 无论多少数据,插入和删除值都只需要非常短的时间,即 O(1)的时间级
- 哈希表的速度比树还要快,基本可以瞬间查找到想要的元素。但是相对于树来说编码要简单得多
相关概念
- 哈希化:将大数字转化成数组范围内下标的过程,称之为哈希化
- 哈希函数:通常会将单词转化成大数字,把大数字进行哈希化的代码实现放在一个函数中,该函数就称为哈希函数
- 哈希表:对最终数据插入的数组进行整个结构的封装,得到的就是哈希表
- 哈希冲突:哈希化过后的下标依然可能重复,产生冲突,冲突是不可避免的,我们只能解决冲突
哈希冲突解决方式
链地址法(拉链法)
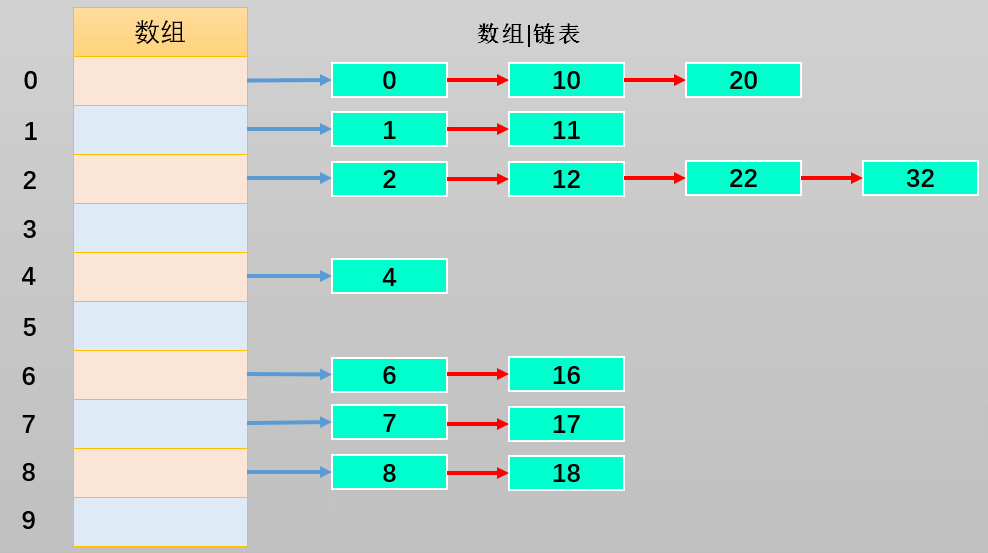
链地址法解决冲突的办法是每个数组单元中存储的不再是单个数据,而是一条链条,这条链条常使用的数据结构为数组或链表,两种数据结构查找的效率相当(因为链条的元素一般不会太多)
- 每一个数字都对 10 进行取余操作,则余数的范围 0~9 作为数组的下标值
- 数组下标对应位置存储的是:由经过取余操作后得到相同余数的数字组成的数组或链表
性能:随着装填因子的增加,平均探测长度呈线性增长,较为平缓。在开发中使用链地址法较多,比如 Java 中的 HashMap 中使用的就是链地址法
开放地址法
开放地址法的主要工作方式是寻找空白的单元格来放置冲突的数据项,具体表现如下图:

根据探测空白单元格位置方式的不同,可分为三种方法:
- 线性探测
- 二次探测
- 再哈希法
线性探测
- 当插入 13 时:对 13 哈希化(对 10 取余)之后得到的下标值 index=3,如果改位置已经存在 33,线性探测就是从 index 位置+1 开始向后依次寻找空的位置放置当前元素 13
- 当查询 13 时:
- 首先 13 经过哈希化得到 index=3,如果 index=3 的位置存放的数据与需要查询的数据 13 相同,就直接返回
- 不相同时,则线性查找,从 index+1 位置开始一个一个位置地查找数据 13
- 查询过程中不会遍历整个哈希表,只要查询到空位置,就停止,因为插入 13 时不会跳过空位置去插入其他位置
- 当删除 13 时:
- 删除操作和上述两种情况类似,但需要注意:不能将该位置下标的内容设置为 null,否则会影响到之后其他的查询操作,因为一遇到为 null 的位置就会停止查找
- 通常删除一个位置的数据项时,我们可以将它进行特殊处理(比如设置为-1),这样在查找时遇到-1 就知道要继续查找
- 线性探测存在的问题:
- 线性探测存在一个比较严重的问题,就是聚集
- 如哈希表中还没插入任何元素时,插入 23、24、25、26、27,这就意味着下标值为 3、4、5、6、7 的位置都放置了数据,这种一连串填充单元就称为聚集
- 聚集会影响哈希表的性能,无论是插入/查询/删除都会影响
- 比如插入 13 时就会发现,连续的单元 3~7 都不允许插入数据,并且在插入的过程中需要经历多次这种情况,即线性查找。二次探测法可以解决该问题
二次探测
- 线性探测:我们可以看成是步长为 1 的探测,比如从下表值 x 开始,那么线性探测就是按照下标值:x+1、x+2、x+3 等依次探测
- 二次探测:对步长进行了优化,比如从下标值 x 开始探测:x+12、x+22、x+33,这样一次性探测比较长的距离,避免了数据聚集带来的影响
- 二次探测存在问题:当插入数据分布性较大的一组数据时,比如:13-163-63-3-213,这种情况会造成步长不一的一种聚集(虽然这种情况出现的概率较线性探测的聚集要小),同样会影响性能
再哈希化
- 在开放地址法中寻找空白单元格的最好的解决方式为再哈希化
- 二次探测的步长是固定的:1,4,9,16 依次类推
- 需要产生一种依赖关键字(数据)的探测序列,而不是每个关键字探测步长都一样
- 即不同的关键字即使映射到相同的数组下标,也可以使用不同的探测序列
- 哈希法的做法为:把关键字用另一个哈希函数,再做一次哈希化,用这次哈希化的结果作为该关键字的步长
- 第二次哈希化需要满足以下两点:
- 和第一个哈希函数不同,不然哈希化后的结果仍是原来位置
- 不能输出为 0,否则每次探测都是原地踏步的死循环
- 优秀的哈希函数:
- stepSize = constant - (key % constant)
- 其中 constant 是质数,且小于数组的容量
- 例如:stepSize = 5 - (key % 5),满足需求,并且结果不可能为 0
- 哈希化的效率
- 哈希表中执行插入和搜索操作效率是非常高的
- 如果没有发生冲突,那么效率就会更高
- 如果发生冲突,存取时间就依赖后来的探测长度
- 平均探测长度以及平均存取时间,取决于填装因子,随着填装因子变大,探测长度会越来越长
- 理解概念-装填因子:
- 装填因子表示当前哈希表中已经包含的数据项和整个哈希表长度的比值
- 装填因子 = 总数据项 / 哈希表长度
- 开放地址法的装填因子最大为 1,因为只有空白的单元才能放入元素
- 链地址法的装填因子可以大于 1,因为只要愿意,拉链法可以无限延伸下去
三种探测性能比较
- 线性探测:随着装填因子的增大,平均探测长度呈指数形式增长,性能较差。实际情况中,最好的装填因子取决于存储效率和速度之间的平衡,随着装填因子变小,存储效率下降,而速度上升
- 二次探测和再哈希法性能相当,它们的性能比线性探测略好。随着装填因子的变大,平均探测长度呈指数形式增长,需要探测的次数也呈指数形式增长,性能不高
两个必备基础
优秀的哈希函数
- 性能高的哈希函数的两个优点:快速的计算和均匀的分布
- 快速的计算:霍纳法则,在中国也叫做秦久韶算法
- 均匀的分布:常量使用质数
快速计算-霍纳法则

- 求多项式的值时,首先计算最内层括号内一次多项式的值,然后由内向外逐层计算一次多项式的值。这种算法把求 n 次多项式 f(x)的值就转化为求 n 个一次多项式的值
- 变换前:乘法次数:n(n+1)/2 次;加法次数:n 次
- 变换后:乘法次数:n 次;加法次数:n 次
- 如果使用大 O 表示时间复杂度的话,直接从变换前的 O(N2)降到了 O(N)
均匀分布-质数
- Java 中的 HashMap 采用的是链地址法,哈希化采用的是公式为:index = HashCode(key)&(Length-1)
- 将数据化为二进制进行与运算,而不是取余运算。这样计算机直接运算二进制数据,效率更高
- 但是 JavaScript 在进行叫大数据的与运算时会出现问题,所以以下使用 JavaScript 实现哈希化时还是采用取余运算
哈希函数代码实现
// 设计哈希函数
// 1. 将字符串转成比较大的数字:hashCode
// 2. 将大的数字hashCode压缩到数组范围之内
function hashFunc(str, size) {
// 1.初始化hashCode的值
var hashCode = 0
// 2.霍纳算法, 来计算hashCode的数值
for (var i = 0; i < str.length; i++) {
hashCode = 37 * hashCode + str.charCodeAt(i)
}
// 3.取模(余)运算
hashCode = hashCode % size
return hashCode
}
console.log(hashFunc("abc", 7)) // 4
console.log(hashFunc("cba", 7)) // 3
console.log(hashFunc("nba", 7)) // 5
console.log(hashFunc("mba", 7)) // 1
质数判断算法
- 质数也称素数
- 质数表示大于 1 的自然数,只能被 1 和自己整除的数
// 方法一:效率较低:根据特点,只能被1和num整除,不能被2 ~ (num-1)整除。遍历2 ~ (num-1)
function isPrime(num) {
// 小于1不用判断
if (num <= 1) {
return false
}
// 循环处理
for (var i = 2; i < num; i++) {
if (num % i == 0) {
return false
}
}
return true
}
// 方法二:效率较高:只需要遍历2 ~ num的平方根即可
// 一个数因式分解,得到的两个数一定是一个小于等于平方根,另一个大于等于平方根
function isPrime(num) {
// 1.获取平方根
var temp = parseInt(Math.sqrt(num))
// 2.循环判断
for (var i = 2; i <= temp; i++) {
if (num % i == 0) {
return false
}
}
return true
}
// 测试
console.log(isPrime(3)) // true
console.log(isPrime(32)) // false
console.log(isPrime(37)) // true
常用操作
- put(key,value):插入或修改操作
- get(key):获取哈希表中特定位置的元素
- remove(key):删除哈希表中特定位置的元素
- isEmpty():如果哈希表中不包含任何元素,返回 true,如果哈希表长度大于 0 则返回 false
- size():返回哈希表包含的元素个数
- resize(value):对哈希表进行扩容操作
哈希表代码实现
封装
图解模型:

实现代码
// 创建HashTable构造函数
function HashTable() {
// 定义属性
this.storage = []
// 计算已经存在的元素
this.count = 0
// 装填因子:loadFactor > 0.75时需要扩容;loadFactor < 0.25时需要减少容量
// 初始长度为7
this.limit = 7
/* 方法 */
// 哈希函数
HashTable.prototype.hashFunc = function (str, size) {
//1.定义hashCode变量
let hashCode = 0
//2.霍纳法则,计算hashCode的值
//cats -> Unicode编码
for (let i = 0; i < str.length; i++) {
// str.charCodeAt(i)//获取某个字符对应的unicode编码
hashCode = 37 * hashCode + str.charCodeAt(i)
}
//3.取余操作
let index = hashCode % size
return index
}
}
put 方法
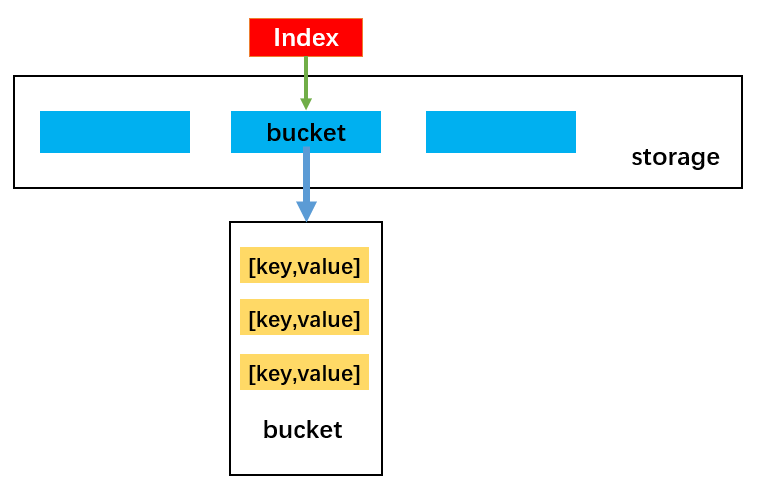
哈希表的插入和修改操作是同一个函数:因为,当使用者传入一个<key,value>时,如果原来不存在该 key,那么就是插入操作,如果原来已经存在该 key,那么就是修改操作。图解如下:
实现思路
- 首先,根据 key 获取索引值 index,目的为将数据插入到 storage 的对应位置
- 然后,根据索引值取出 bucket,如果 bucket 不存在,先创建 bucket,随后放置在该索引值的位置
- 接着,判断新增还是修改原来的值。如果已经有值了,就修改该值;如果没有,就执行后续操作
- 最后,进行新增数据操作
实现代码#
// put方法:插入|修改操作
HashTable.prototype.put = function (key, value) {
// 1.根据key获取对应的index
var index = this.hashFunc(key, this.limit)
// 2.根据index取出对应的bucket
// 数组中放置数据的方式: [[ [k,v], [k,v], [k,v] ] , [ [k,v], [k,v] ] [ [k,v] ] ]
var bucket = this.storage[index]
// 3. 判断该bucket是否为null
if (bucket == null) {
// 创建bucket
bucket = []
this.storage[index] = bucket
}
// 4. 判断是新增还是修改原来的值
for (var i = 0; i < bucket.length; i++) {
var tuple = bucket[i]
if (tuple[0] == key) {
// 修改
tuple[1] = value
return //不用返回值
}
}
// 5.进行添加操作
bucket.push([key, value])
this.count += 1
}
测试
// 1.创建哈希表
var ht = new HashTable()
// 2.插入数据
ht.put("abc", "123")
ht.put("cba", "321")
ht.put("nba", "521")
ht.put("mba", "520")
console.log(ht) // HashTable {storage: Array(6), count: 4, limit: 7}
get 方法
实现思路
- 首先,根据 key 通过哈希函数获取它在 storage 中对应的索引值 index
- 然后,根据索引值获取对应的 bucket
- 接着,判断获取到的 bucket 是否为 null,如果为 null,直接返回 null
- 随后,线性遍历 bucket 中每一个 key 是否等于传入的 key。如果等于,直接返回对应的 value
- 最后,遍历完 bucket 后,仍然没有找到对应的 key,直接 return null 即可
实现代码
// get方法:获取元素
HashTable.prototype.get = function (key) {
// 1.根据key获取对应的index
var index = this.hashFunc(key, this.limit)
// 2.根据index取出对应的bucket
var bucket = this.storage[index]
// 3. 判断该bucket是否为null,如果bucket为null, 那么说明这个位置没有数据
if (bucket == null) {
return null
}
// 4. 有bucket,那么就进行线性查找
for (var i = 0; i < bucket.length; i++) {
var tuple = bucket[i]
// tuple[0]存储key,tuple[1]存储value
if (tuple[0] == key) {
return tuple[1]
}
}
// 5.依然没有找到,那么返回null
return null
}
测试
// 3.获取数据
console.log(ht.get("abc")) // 123
console.log(ht.get("cba")) // 321
console.log(ht.get("nba")) // 521
remove 方法
实现思路
- 首先,根据 key 通过哈希函数获取它在 storage 中对应的索引值 index
- 然后,根据索引值获取对应的 bucket
- 接着,判断获取到的 bucket 是否为 null,如果为 null,直接返回 null
- 随后,线性查找 bucket,寻找对应的数据,并且删除
- 最后,依然没有找到,返回 null
实现代码
// remove方法:删除操作
HashTable.prototype.remove = function (key) {
// 1.根据key获取对应的index
var index = this.hashFunc(key, this.limit)
// 2.根据index取出对应的bucket
var bucket = this.storage[index]
// 3. 判断该bucket是否为null,如果bucket为null, 那么说明这个位置没有数据
if (bucket == null) {
return null
}
// 4. 有bucket,那么就进行线性查找并删除
for (var i = 0; i < bucket.length; i++) {
var tuple = bucket[i]
if (tuple[0] == key) {
bucket.splice(i, 1)
this.count -= 1
return tuple[1]
}
}
// 5.依然没有找到,那么返回null
return null
}
测试
// 4.删除数据
console.log(ht.remove("abc")) // 123
console.log(ht.remove("mba")) // 520
console.log(ht) // HashTable {storage: Array(6), count: 2, limit: 7}
isEmpty | size 方法
实现代码
// isEmpty方法:判断是否为空
HashTable.prototype.isEmpty = function (key) {
return this.count == 0
}
// size方法:获取元素的个数
HashTable.prototype.size = function (key) {
return this.count
}
测试
// 5. 其他方法
console.log(ht.isEmpty()) // false
console.log(ht.size()) // 4
扩容与压缩
为什么需要扩容和压缩
- 由于使用的是链地址法,装填因子(loadFactor)可以大于 1,所以这个哈希表可以无限制地插入新数据
- 随着数据量的增多,storage 中每一个 index 对应的 bucket 数组(链表)就会越来越长,会造成哈希表效率的降低
- 随着删除数据的操作变多,空闲空间也会变多,需要压缩长度来提高查询效率
扩容和压缩条件
- 当装填因子 laodFactor > 0.75 时,对哈希表进行扩容
- 当装填因子 laodFactor < 0.25 时,对哈希表容量进行压缩
实现思路
步骤
- 首先,定义一个变量,比如 oldStorage 指向原来的 storage
- 然后,创建一个新的容量更大的数组,让 this.storage 指向它
- 最后,将 oldStorage 中的每一个 bucket 中的每一个数据取出来依次添加到 this.storage 指向的新数组中
图解
实现代码
// resize方法:扩容和压缩的长度改变
HashTable.prototype.resize = function (newLimit) {
// 1.保存旧的storage数组内容
var oldStorage = this.storage
// 2. 重置所有的属性
this.storage = []
this.count = 0
this.limit = newLimit
// 3.遍历oldStorage中所有的bucket
for (var i = 0; i < oldStorage.length; i++) {
// 3.1 取出对应的bucket
var bucket = oldStorage[i]
// 3.2.判断bucket是否为null
if (bucket === null) {
continue
}
// /3.3.bucket中有数据,就取出数据重新插入
for (var j = 0; j < bucket.length; j++) {
var tuple = bucket[j]
this.put(tuple[0], tuple[1]) //插入数据的key和value
}
}
}
条件代码 装填因子 = 哈希表中数据 / 哈希表长度,即 loadFactor = count / HashTable.length
(1) 通常情况下当装填因子 laodFactor > 0.75 时,对哈希表进行扩容。在哈希表中的添加方法(put 方法)中添加如下代码,判断是否需要调用扩容函数进行扩容:
//判断是否需要扩容操作
if (this.count > this.limit * 0.75) {
this.resize(this.limit * 2)
}
(2) 当装填因子 laodFactor < 0.25 时,对哈希表容量进行压缩。在哈希表中的删除方法(remove 方法)中添加如下代码,判断是否需要调用扩容函数进行压缩:
//缩小容量
if (this.limit > 7 && this.count < this.limit * 0.25) {
this.resize(Math.floor(this.limit / 2))
}
质数作为容量
实现思路
- 2 倍扩容之后,通过循环调用 isPrime 判断得到的容量是否为质数,不是则+1,直到是为止
- 比如原长度:7,2 倍扩容后长度为 14,14 不是质数,14 + 1 = 15 不是质数,15 + 1 = 16 不是质数,16 + 1 = 17 是质数,停止循环,由此得到质数 17
实现代码
// isPrime方法:高效判断质数方法
HashTable.prototype.isPrime = function (num) {
// 小于1不用判断
if (num <= 1) {
return false
}
// 1.获取平方根
var temp = parseInt(Math.sqrt(num))
// 2.循环判断
for (var i = 2; i <= temp; i++) {
if (num % i == 0) {
return false
}
}
return true
}
// getPrime方法:获取质数
HashTable.prototype.getPrime = function (num) {
// 7*2=14,+1=15,+1=16,+1=17(质数)
while (!this.isPrime(num)) {
num++
}
return num
}
put 和 remove 中加入条件
// put方法中加入: 判断是否需要扩容操作
if (this.count > this.limit * 0.75) {
let newSize = this.limit * 2
let newPrime = this.getPrime(newSize)
this.resize(newPrime)
}
// remove方法中加入: 判断是否需要减小容量操作
if (this.limit > 7 && this.count < this.limit * 0.25) {
let newSize = Math.floor(this.limit / 2)
let newPrime = this.getPrime(newSize)
this.resize(newPrime)
}
完整代码
// 创建HashTable构造函数
function HashTable() {
// 定义属性
this.storage = []
// 计算已经存在的元素
this.count = 0
// 装填因子:loadFactor > 0.75时需要扩容;loadFactor < 0.25时需要减少容量
// 初始长度为7
this.limit = 7
/* 方法 */
// 哈希函数
HashTable.prototype.hashFunc = function (str, size) {
// 1.初始化hashCode的值
var hashCode = 0
// 2.霍纳算法, 来计算hashCode的数值
for (var i = 0; i < str.length; i++) {
hashCode = 37 * hashCode + str.charCodeAt(i)
}
// 3.取模(余)运算
hashCode = hashCode % size
return hashCode
}
// put方法:插入|修改操作
HashTable.prototype.put = function (key, value) {
// 1.根据key获取对应的index
var index = this.hashFunc(key, this.limit)
// 2.根据index取出对应的bucket
// 数组中放置数据的方式: [[ [k,v], [k,v], [k,v] ] , [ [k,v], [k,v] ] [ [k,v] ] ]
var bucket = this.storage[index]
// 3. 判断该bucket是否为null
if (bucket == null) {
// 创建bucket
bucket = []
this.storage[index] = bucket
}
// 4. 判断是新增还是修改原来的值
for (var i = 0; i < bucket.length; i++) {
var tuple = bucket[i]
if (tuple[0] == key) {
// 修改
tuple[1] = value
return //不用返回值
}
}
// 5.进行添加操作
bucket.push([key, value])
this.count += 1
// 6.判断是否需要扩容操作
if (this.count > this.limit * 0.75) {
let newSize = this.limit * 2
let newPrime = this.getPrime(newSize)
this.resize(newPrime)
}
}
// get方法:获取元素
HashTable.prototype.get = function (key) {
// 1.根据key获取对应的index
var index = this.hashFunc(key, this.limit)
// 2.根据index取出对应的bucket
var bucket = this.storage[index]
// 3. 判断该bucket是否为null,如果bucket为null, 那么说明这个位置没有数据
if (bucket == null) {
return null
}
// 4. 有bucket,那么就进行线性查找
for (var i = 0; i < bucket.length; i++) {
var tuple = bucket[i]
// tuple[0]存储key,tuple[1]存储value
if (tuple[0] == key) {
return tuple[1]
}
}
// 5.依然没有找到,那么返回null
return null
}
// remove方法:删除操作
HashTable.prototype.remove = function (key) {
// 1.根据key获取对应的index
var index = this.hashFunc(key, this.limit)
// 2.根据index取出对应的bucket
var bucket = this.storage[index]
// 3.判断该bucket是否为null,如果bucket为null, 那么说明这个位置没有数据
if (bucket == null) {
return null
}
// 4.有bucket,那么就进行线性查找并删除
for (var i = 0; i < bucket.length; i++) {
var tuple = bucket[i]
if (tuple[0] == key) {
bucket.splice(i, 1)
this.count -= 1
// 6.缩小容量
if (this.limit > 7 && this.count < this.limit * 0.25) {
let newSize = Math.floor(this.limit / 2)
let newPrime = this.getPrime(newSize)
this.resize(newPrime)
}
return tuple[1]
}
}
// 5.依然没有找到,那么返回null
return null
}
// isEmpty方法:判断是否为空
HashTable.prototype.isEmpty = function (key) {
return this.count == 0
}
// size方法:获取元素的个数
HashTable.prototype.size = function (key) {
return this.count
}
// resize方法:扩容和压缩的长度改变
HashTable.prototype.resize = function (newLimit) {
// 1.保存旧的storage数组内容
var oldStorage = this.storage
// 2. 重置所有的属性
this.storage = []
this.count = 0
this.limit = newLimit
// 3.遍历oldStorage中所有的bucket
for (var i = 0; i < oldStorage.length; i++) {
// 3.1 取出对应的bucket
var bucket = oldStorage[i]
// 3.2.判断bucket是否为null
if (bucket == null) {
continue
}
// /3.3.bucket中有数据,就取出数据重新插入
for (var j = 0; j < bucket.length; j++) {
var tuple = bucket[j]
this.put(tuple[0], tuple[1]) //插入数据的key和value
}
}
}
// isPrime方法:高效判断质数方法
HashTable.prototype.isPrime = function (num) {
// 小于1不用判断
if (num <= 1) {
return false
}
// 1.获取平方根
var temp = parseInt(Math.sqrt(num))
// 2.循环判断
for (var i = 2; i <= temp; i++) {
if (num % i == 0) {
return false
}
}
return true
}
// getPrime方法:获取质数
HashTable.prototype.getPrime = function (num) {
// 7*2=14,+1=15,+1=16,+1=17(质数)
while (!this.isPrime(num)) {
num++
}
return num
}
}
// 测试哈希表
// 1.创建哈希表
var ht = new HashTable()
// 2.插入数据
ht.put("abc", "123")
ht.put("cba", "321")
ht.put("nba", "521")
ht.put("mba", "520")
console.log(ht) // HashTable {storage: Array(6), count: 4, limit: 7}
// 3.获取数据
console.log(ht.get("abc")) // 123
console.log(ht.get("cba")) // 321
console.log(ht.get("nba")) // 521
// 4.删除数据
console.log(ht.remove("abc")) // 123
console.log(ht.remove("mba")) // 520
console.log(ht) // HashTable {storage: Array(6), count: 2, limit: 7}
// 5. 其他方法
console.log(ht.isEmpty()) // false
console.log(ht.size()) // 2
// 测试扩容
var ht2 = new HashTable()
ht2.put("class1", "1")
ht2.put("class2", "2")
ht2.put("class3", "3")
ht2.put("class4", "4")
ht2.put("class5", "5")
ht2.put("class6", "6")
ht2.put("class7", "7")
ht2.put("class8", "8")
ht2.put("class9", "9")
ht2.put("class10", "10")
console.log(ht2) // HashTable {storage: Array(17), count: 10, limit: 17}
console.log(ht2.size()) //10
console.log(ht2.limit) //17